Eitt af megináskorunum fyrirtækja í smásölu í dag er ekki bara að auka tekjur sínar, minnka brottfall og bjóða upp á vöruúrval sem hentar flestum heldur er að það að þekkja viðskiptavin sinn. Með því að þekkja hegðun hans getum við stýrt markaðsherferðum betur, haft betri hugmynd um hvaða vörur við ættum að bjóða upp á, fáum sterka röksemd hvernig við getum krossselt vörur okkar en heilt yfir getum við bætt upplifun okkar viðskiptavina. Ein algengasta leið til að ná að skilja hegðunarmynstur viðskiptavina er með svokallaðri þyrpanagreiningu (e. clustering) sem er algeng reikniaðferð í vélanámi (e. machine learning). Þessi reikniaðferð er það sem kallað er unsupervised sem þýðir að við getum í rauninni ekki með skilvirkum hætti metið hversu góðri afurð líkanið skilar af sér.
Í grunninn er þetta nokkuð einfalt markmið – við viljum nota þessa reikniaðferð til að skipta okkar viðskiptavinahóp í nokkra hópa þar sem viðskiptavinir hvers og eins hóps deila sömu hegðunarmynstri.

Til þess að greiningin skili tilætluðum árangri þarf að rannsaka hvaða eigindi skal skoða fyrir okkar viðskiptavini og fara þau eftir hverju og einu fyrirtæki fyrir sig. Þessi eigindi geta verið allt á milli himins og jarðar, s.s. hvaða vöruflokka viðskiptavinur er að versla, hversu oft verslar viðkomandi, hvað á hann mörg börn, lengd viðskiptasambands, meðalupphæð á reikningi, meðalfjöldi vara o.s.frv. Þegar búið er að ákveða hvaða eigindi skal nota, sem geta verið mörg eða fá, þá er hægt að fara að smíða líkan sem skiptir viðskiptavinunum í flokka. Það má bæta við að bæði geta eigindin verið töluleg (e. numerical) eða flokkunar (e. categorical).
Það skiptir einnig miklu máli í svona greiningu að forvinna gögnin með skilvirkum hætti – það þarf að fjarlægja einfara (e. outliers), taka afstöðu fyrir tóm gildi (hægt að fjarlægja eða setja eitthvað í staðinn t.d. meðaltal) og þegar velja á eigindin þurfa þau að stuðla að því markmiði sem sett er upp með með þyrpanagreiningunni í upphafi. Ennfremur þarf að skala gögnin þannig að hvert eigindi spanni sama bil af tölum – getum tekið hér sem dæmi aldur og upphæðir á reikningi. Upphæðirnar ná mögulega upp í mörg hundruð þúsund meðan aldurinn nær aldrei yfir 80, með skölun tökum við þetta til greina og þetta bjagar ekki reikningana hjá líkaninu. Að lokum má nefna að það getur verið þess virði að gera PCA greiningu en í henni drögum við úr fjölda eiginda og skiljum eftir þau eigindi sem skipta máli. Þetta getur hraðað á gagnavinnslu líkansins sem skiptir miklu máli í heildarsamhenginu.
Þyrpanalíkön eru jafn mismunandi og þau eru mörg og reiknirit þeirra misflókin. Í þessari færslu ætla ég að fara yfir þrjú helstu reiknirit sem hafa sína kosti og galla; KMeans, Hierarchical og DBSCAN.
KMeans
Eitt vinsælasta reikniritið sem þið finnið í öllum námskeiðum í gervigreind um allan heim er KMeans reikniritið sem skiptir ómerktu (e. unlabeled) gagnasafni í mismunandi þyrpingar. Fjöldi þyrpinga er tala sem þarf að ákvarða meðan á ferlinu stendur , ef K=2 þá skiptum við því sem um ræðir í tvær þyrpingar.
Reikniritið gerir í grunninn eftirfarandi:
- Af handahófi, velja K punkta í gagnasafninu sem miðjur hvers þyrpingar.
- Fyrir hvern punkt í gagnasafninu okkar, reiknum fjarlægðina að hverri miðju og merking hvers punkts er úthlutað út frá þeirri miðju sem er honum næst. Yfirleitt er notast við evklíðska fjarlægðarformið þegar fjarlægðin er reiknuð en hægt er að nota fleiri.
- Þegar öllum punktum hefur verið úthlutað hóp, endurreiknum miðju hvers og eins hóps út frá meðaltali þeirra. Þetta skref lagar til miðju hvers hóps en í upphafi er hún sett af handahófi.
- Þegar búið er að reikna nýja miðju, þá endurtökum við reikningana með því að úthluta þyrpingu fyrir hvern og einn punkt útfrá fjarlægð þeirra til miðju þyrpinga. Þetta er svo endurtekið aftur og aftur þangað til að punktar hætta nokkurn veginn að fá úthlutað nýjan hóp.
- Reikniritið hættir þegar miðjur þyrpina hafa náð jafnvægi
Hierarchical Clustering
Þessi reikniaðferð er tegund þyrpanagreiningar sem leitast við að búa til stigveldi af þyrpunum. Ólíkt KMeans sem við töluðum um hér fyrir ofan, þar sem nauðsynlegt er að segja fyrirfram hversu margar þyrpanir þú ætlar að fá, þá er þess ekki þörf í þessari nálgun. Í staðinn, þá útbýr reikniritið til eins konar tré (e. dendrogram) sem lýsir niðurstöðum reikniritsins á skiljanlegan hátt.
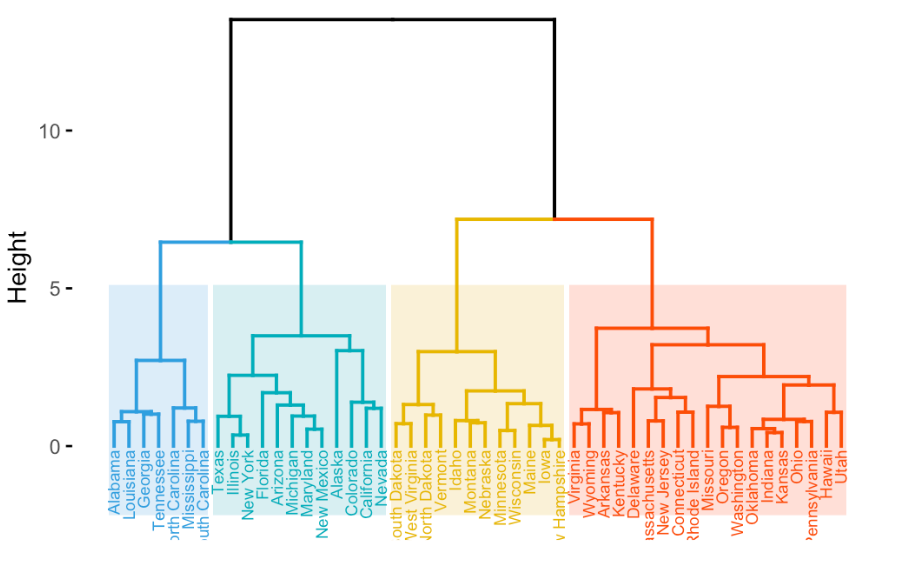
Það skiptir miklu máli í þessu reikniriti, eins og öðrum þyrpanareikniritum, hvernig á að meta fjarlægðir. Eins og áður var nefnt þekkja flesta hina klassísku evklíðsku fjarlægð (e. Euclidean distance) sem er hagnýt þegar gögnin eru samfelld, normaldreifð og töluleg en hægt er að nota t.d. Manhattan fjarlægð þegar gögnin eru flokkunar (e. categorical) eða tvístæð (e. binary). Í þessu reikniriti eru báðar fjarlægðir notaðar og getur haft töluverð áhrif á lokaniðurstöður. Aðrar fjarlægðir sem minnast má á eru Pearson fylgni (e. Pearson correlation) eða kósínus einslögun (e. cosine similarity) en hvað skal velja sem fjarlægð fer eftir eðli gagnanna.
Hierarchical Clustering er oft notað þegar gagnasafnið sem við erum að notast við er lítið eða millistórt – ef gagnasafnið er í stærra laginu geta reikningarnir orðið ansi dýrir. Hægt er að nota þessa reikniaðferð bæði fyrir flokkunargögn og númerísk gögn en Manhattan fjarlægð er oft notuð fyrir flokkunar- og tvístæð gögn meðan Evklíðska fjarlægðin er notuð fyrir töluleg gögn. Þetta er öflug reikniaðferð fyrir að skoða og kynnast mynstrinu í gögnunum sem fást er við – sér í lagi vegna þess að það er óþarfi að segja fyrirfram hve margar þyrpanir eru í gagnasafninu eins og í KMeans reikniritinu.
DBSCAN

